What is the difference between skewness and kurtosis?
Skewness and kurtosis are both important measures of a distribution’s shape.
- Skewness measures the asymmetry of a distribution.
- Kurtosis measures the heaviness of a distribution’s tails relative to a normal distribution.
What are the three categories of kurtosis?
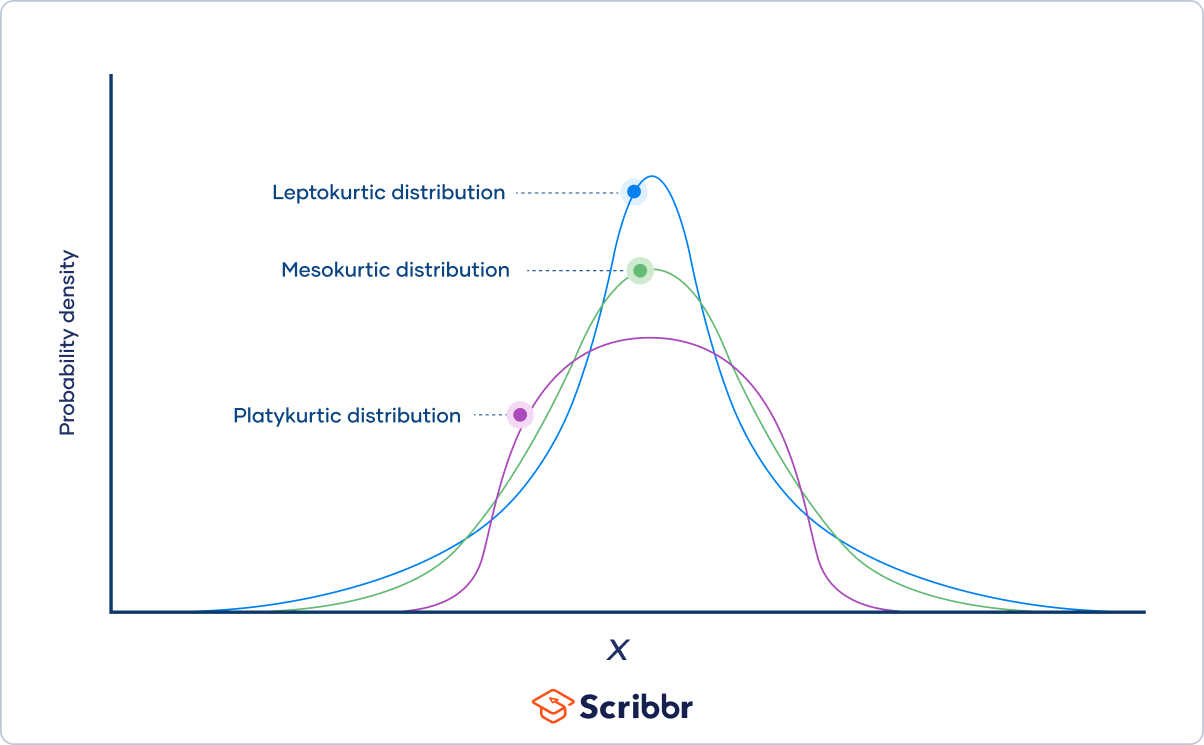
The three categories of kurtosis are:
- Mesokurtosis: An excess kurtosis of 0. Normal distributions are mesokurtic.
- Platykurtosis: A negative excess kurtosis. Platykurtic distributions are thin-tailed, meaning that they have few outliers.
- Leptokurtosis: A positive excess kurtosis. Leptokurtic distributions are fat-tailed, meaning that they have many outliers.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2024, January 29). What Is Kurtosis? | Definition, Examples & Formula. Scribbr. Retrieved March 17, 2025, from https://www.scribbr.com/statistics/kurtosis/
Other students also liked
Skewness | Definition, Examples & Formula
Skewness is a measure of the asymmetry of a distribution. A distribution can have right (or positive), left (or negative), or zero skewness.
Parameter vs Statistic | Definitions, Differences & Examples
A parameter is a number that describes a whole population, while a statistic is a number that describes a sample.
Frequency Distribution | Tables, Types & Examples
A frequency distribution is the number of observations for each possible value of a variable.
