What is a mesokurtic distribution?
Types of kurtosis
Distributions can be categorized into three groups based on their kurtosis:
| Category | |||
|---|---|---|---|
| Mesokurtic | Platykurtic | Leptokurtic | |
| Tailedness | Medium-tailed | Thin-tailed | Fat-tailed |
| Outlier frequency | Medium | Low | High |
| Kurtosis | Moderate (3) | Low (< 3) | High (> 3) |
| Excess kurtosis | 0 | Negative | Positive |
| Example distribution | Normal | Uniform | Laplace |
What is a mesokurtic distribution?
A mesokurtic distribution is medium-tailed, so outliers are neither highly frequent, nor highly infrequent.
Kurtosis is measured in comparison to normal distributions.
- Normal distributions have a kurtosis of 3, so any distribution with a kurtosis of approximately 3 is mesokurtic.
Often, kurtosis is described in terms of excess kurtosis, which is kurtosis − 3. Since normal distributions have a kurtosis of 3, excess kurtosis makes comparing a distribution’s kurtosis to a normal distribution even easier:
- Normal distributions have an excess kurtosis of 0, so any distribution with an excess kurtosis of approximately 0 is mesokurtic.
Mesokurtic distribution example
On average, a female baby elephant weighs an impressive 210 lbs at birth. Suppose that a zoologist is interested in the distribution of elephant birth weights, so she contacts zoos and sanctuaries around the world and asks them to share their data. She collects birth weight data for 400 female baby elephants:
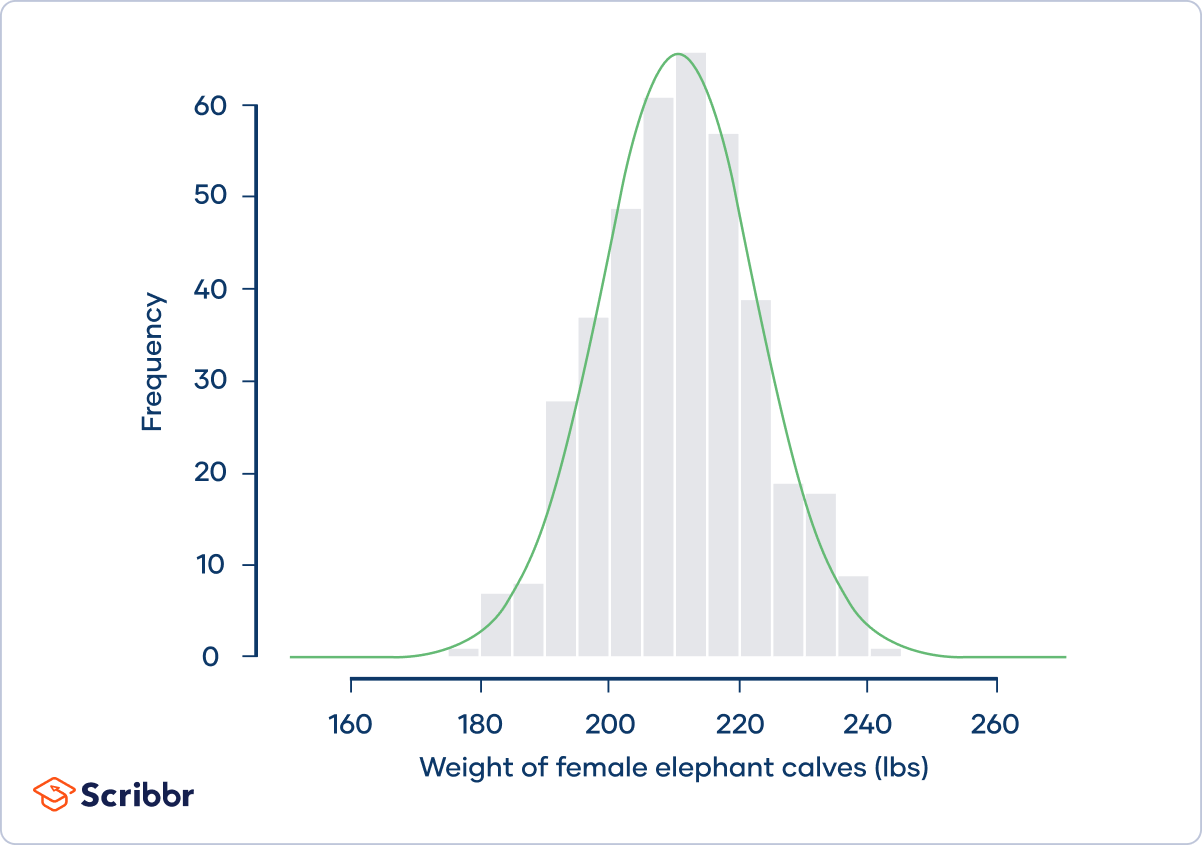
From the graph, we can see that the frequency distribution (shown by the gray bars) approximately follows a normal distribution (shown by the green curve). Normal distributions are mesokurtic.
The zoologist calculates the kurtosis of the sample. She finds that the kurtosis is 3.09 and the excess kurtosis is 0.09, and she concludes that the distribution is mesokurtic.
Mesokurtic distributions have outliers that are neither highly frequent, nor highly infrequent, and this is true of the elephant birth weights.