What is a platykurtic distribution?
What is a platykurtic distribution?
A platykurtic distribution is thin-tailed, meaning that outliers are infrequent.
Platykurtic distributions have less kurtosis than a normal distribution. In other words, platykurtic distributions have:
- A kurtosis of less than 3
- An excess kurtosis of less than 0
Platykurtosis is sometimes called negative kurtosis, since the excess kurtosis is negative.
A trick to remember the meaning of “platykurtic” is to think of a platypus with a thin tail.
Platykurtic distribution example
A sociologist is studying the social media use of students at a small high school. There are 400 students at the school, ranging in age from 14 to 18 years old:
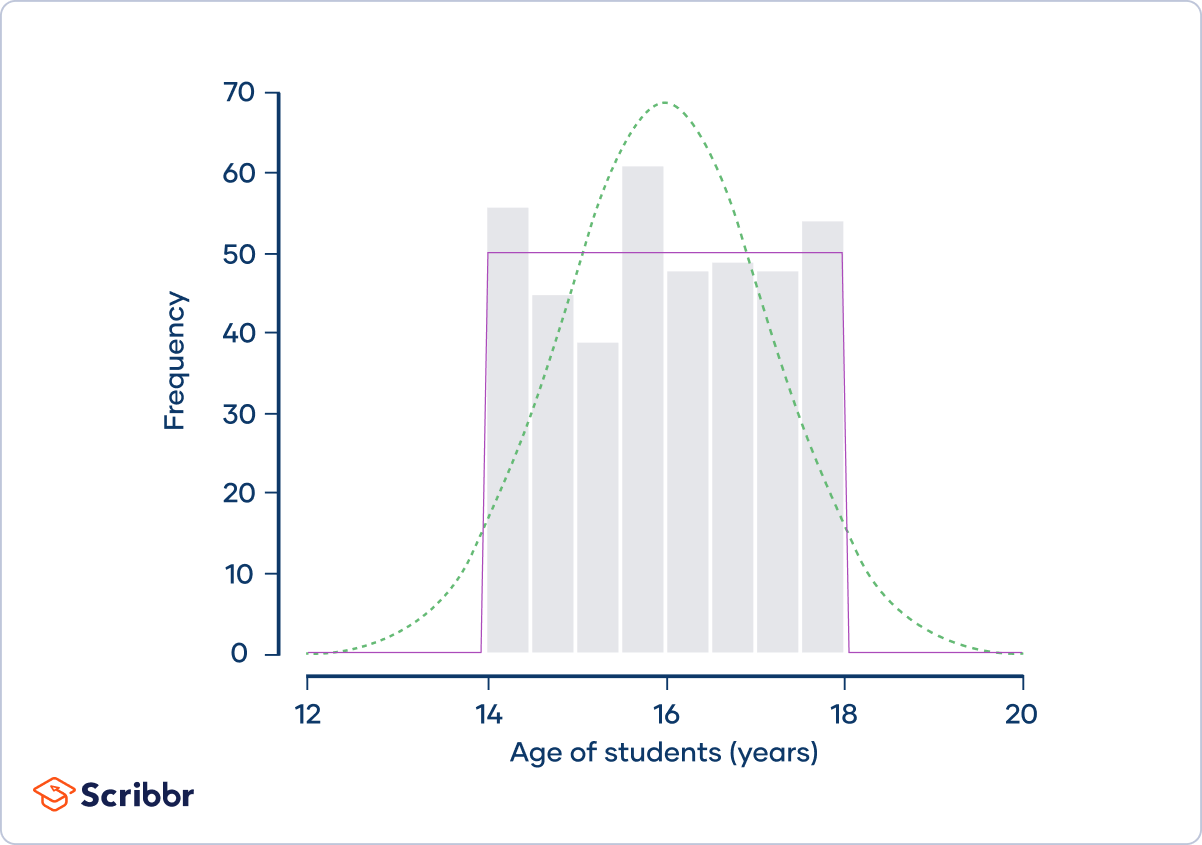
The frequency distribution (shown by the gray bars) doesn’t follow a normal distribution (shown by the dotted green curve). Instead, it approximately follows a uniform distribution (shown by the purple curve). Uniform distributions are platykurtic.
The sociologist calculates that the kurtosis of the sample is 1.78 and its excess kurtosis is −1.22. He concludes that the distribution is platykurtic.
Platykurtic distributions have a low frequency of outliers. Uniform distributions, like the distribution of students’ ages, are the extreme cases of platykurtic distributions because outliers are so rare that they’re completely absent. There are no students younger than 14 or older than 18 years.