What does a correlation coefficient tell you?

Correlation coefficients summarize data and help you compare results between studies.

Summarizing data

A correlation coefficient is a descriptive statistic. That means that it summarizes sample data without letting you infer anything about the population. A correlation coefficient is a bivariate statistic when it summarizes the relationship between two variables, and it’s a multivariate statistic when you have more than two variables.

If your correlation coefficient is based on sample data, you’ll need an inferential statistic if you want to generalize your results to the population. You can use an F test or a t test to calculate a test statistic that tells you the statistical significance of your finding.

Comparing studies

A correlation coefficient is also an effect size measure, which tells you the practical significance of a result.

Correlation coefficients are unit-free, which makes it possible to directly compare coefficients between studies.

Here’s why students love Scribbr’s proofreading services

Discover proofreading & editing

Using a correlation coefficient

In correlational research, you investigate whether changes in one variable are associated with changes in other variables.

Correlational research example

You investigate whether standardized scores from high school are related to academic grades in college. You predict that there’s a positive correlation: higher SAT scores are associated with higher college GPAs while lower SAT scores are associated with lower college GPAs.

After data collection, you can visualize your data with a scatterplot by plotting one variable on the x-axis and the other on the y-axis. It doesn’t matter which variable you place on either axis.

Visually inspect your plot for a pattern and decide whether there is a linear or non-linear pattern between variables. A linear pattern means you can fit a straight line of best fit between the data points, while a non-linear or curvilinear pattern can take all sorts of different shapes, such as a U-shape or a line with a curve.

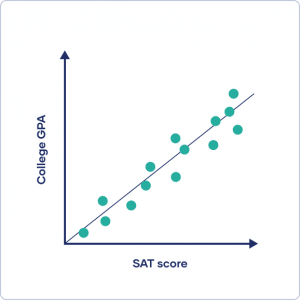
Inspecting a scatterplot for a linear pattern — Visual inspection example

There are many different correlation coefficients that you can calculate. After removing any outliers, select a correlation coefficient that’s appropriate based on the general shape of the scatter plot pattern. Then you can perform a correlation analysis to find the correlation coefficient for your data.

You calculate a correlation coefficient to summarize the relationship between variables without drawing any conclusions about causation.

Correlation analysis example

You check whether the data meet all of the assumptions for the Pearson’s r correlation test.

Both variables are quantitative and normally distributed with no outliers, so you calculate a Pearson’s r correlation coefficient.

The correlation coefficient is strong at .58.